Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Solve 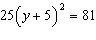 by the Square Root Property, if
possible.
|
|
|
2.
|
Solve 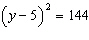 by the Square Root Property, if
possible.
|
|
|
3.
|
Solve the equation by using the Square Root Property.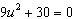 
|
|
|
4.
|
Find all real and complex solutions of the quadratic equation  .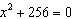
|
|
|
5.
|
Find all real and complex solutions of the quadratic equation  .
|
|
|
6.
|
Solve the equation of quadratic form.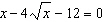 
|
|
|
7.
|
Solve the equation 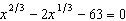 . (Find all real and complex
solutions.)
|
|
|
8.
|
What term should be added to 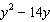 to make it a perfect square
trinomial?
|
|
|
9.
|
Solve 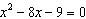 by completing the square, if possible.
|
|
|
10.
|
Solve 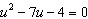 by completing the square, if possible.
|
|
|
11.
|
Solve the equation 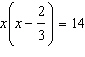 by completing the square. Give the solutions
in exact form and in decimal form rounded to two decimal places. (The solutions may be complex
numbers.)
|
|
|
12.
|
Use the Quadratic Formula to solve  .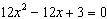
|
|
|
13.
|
Solve  .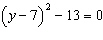
|
|
|
14.
|
Use the Quadratic Formula to solve 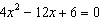 , if possible. Round your
answer(s) to two decimal places.
|
|
|
15.
|
Write the quadratic equation having solutions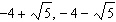 
|
|
|
16.
|
Find the vertex of  .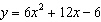
|
|
|
17.
|
Find the intercepts of 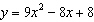 . a. | x-intercept: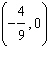 
y-intercepts: 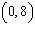 | b. | no x-intercepts
y-intercept: 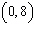 | c. | x-intercept: 
no
y-intercepts | d. | no x-intercepts
y-intercept:
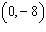 | e. | x-intercept:
y-intercept:  |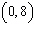
|
|
|
18.
|
If the area of a rectangle is 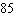 square meters, and the
width is ten meters shorter than the length, find the perimeter of the rectangle in meters. Round
your answer to two decimal places. a. |  meters | b. | 
meters | c. |  meters | d. | 
meters | e. |  meters |
|
|
|
19.
|
The height h (in feet) of a falling object above the ground at time
t (in seconds) is modeled by 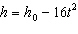 , where 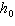 is the
initial height. Find the time (in seconds) it takes for an object to fall to the ground if the
initial height is 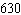 feet. Round your answer to two decimal
places. a. |  seconds | b. | 
seconds | c. |  seconds | d. | 
seconds | e. |  seconds |
|
|
|
20.
|
Use a graphing calculator to approximate the values of x that satisfy the
inequality  .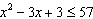
|